Getting it Right: Solving GHSA challenges with math, Part VI

In the first five parts of the series, we've only used a single formula – Rothman Grading as introduced in Part III and explored in Part IV, which I know you've been practicing :-)

So today let’s roll up our sleeves and get our hands dirty with a couple of more formulas. Don’t worry -- Rothman Grading is by far the most complicated formula in the Extended Standings, so if you’re comfortable with that then the rest will be exceedingly easy.

To start, let's return to the concept of pairwise comparison. In Part III, I mentioned how L.L. Thurstone provided the theoretical basis for pairwise comparison and even presented a probability model to scale and order (i.e., rate and rank) items compared in pairs. Thurstone's probability model was somewhat math heavy, but in 1952 R.A. Bradley and M.E. Terry presented a wonderfully simple alternative.

In their model, the probability that A is preferred to B is:

A / (A + B)

Today this is widely known as the "Bradley-Terry" (B-T) model, so we'll refer to this formula, our first of the day, as the B-T Probability Function.

For those interested, Ernst Zermelo actually presented this model in 1929. However, it was apparently forgotten by academia, leaving it to be rediscovered by Bradley and Terry. Some have attempted to correct this perceived injustice by referring to it as the "Zermelo” model.

At any rate, the B-T model has endured and even been expanded in several directions over the last six decades.  Use of it today for the Extended Standings is simply another application.

So let’s look under the hood of the B-T model by working through an example from last season’s Archer, Dacula, and Grayson teams that went 1-1 against each other.  We'll pretend this is a three team league participating in a "round robin" tournament and ignore all other GHSA teams and games.

We’ll build two tables for this exercise, one for the teams and one for the games. The Extended Standings will be the result of the iterative interaction between these two tables.

Let’s start our team table with headings for “Rating”, “Adjusted Wins”, “Total Denominator”, and “Updated Ratings”.

We’ll also assign an initial rating to all teams. Technically it could be any number, but by convention the lowest rating in the B-T model is always 1, so we’ll assign all teams an initial rating of 1.

Now let’s build our games table to show the game data and include headers for the “Rothman Grade” and the “Rating” for each team and also add a column that we’ll call the “Denominator”, which is simply 1 / (Team rating + Opponent rating).  Currently, because all the team ratings are at 1, then every Denominator is 1 / (Team rating + Opponent rating) = 1 / (1 + 1) = 0.500, but will change as the team ratings change.

So right now everything looks like this:

Credit: Loren Maxwell

Credit: Loren Maxwell

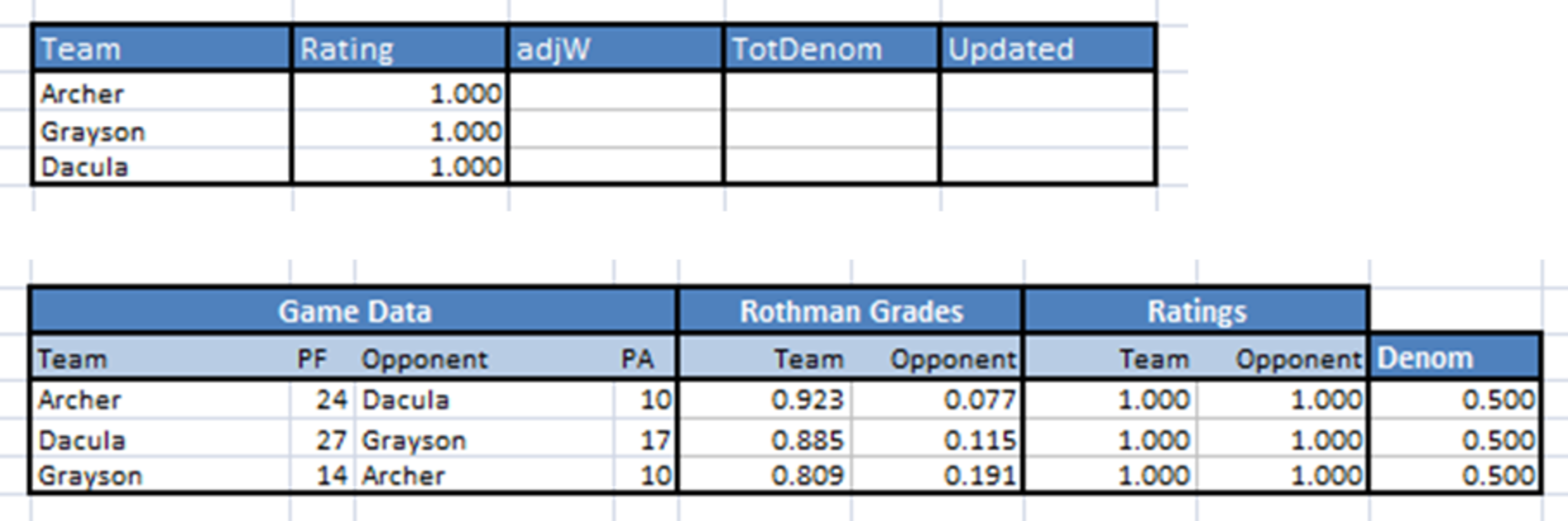
Now, let’s revisit the team table to update the Adjusted Wins and the Total Denominator for each team.  For Adjusted Wins we simply total the team's Rothman Grade for each game.  For example, Archer gets 0.923 Adjusted Wins from their game against Dacula and another 0.191 Adjusted Wins from their game against Grayson for a total of 1.113 Adjusted Wins. Also, let’s update the Total Denominator by adding all the Denominators from each game a team was involved in.  Since each team played in two games, each team’s Total Denominator will be 0.500 + 0.500 = 1.000.

Now our tables look like this:

Credit: Loren Maxwell

Credit: Loren Maxwell

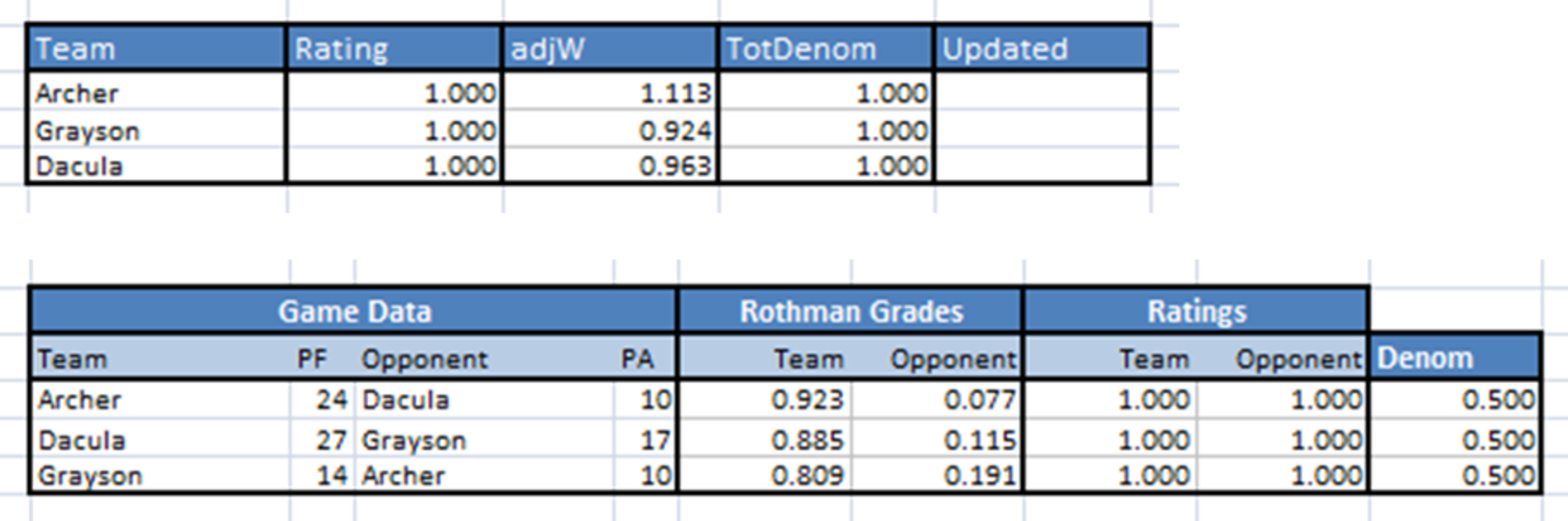
Everything has been filled out except the Updated Rating in the team table, so let's introduce our second formula of the day, which we'll call the B-T Update Function. The B-T Update Function is the amazingly simple:

Adjusted Wins / Total Denominator

So our team table becomes:

Credit: Loren Maxwell

Credit: Loren Maxwell

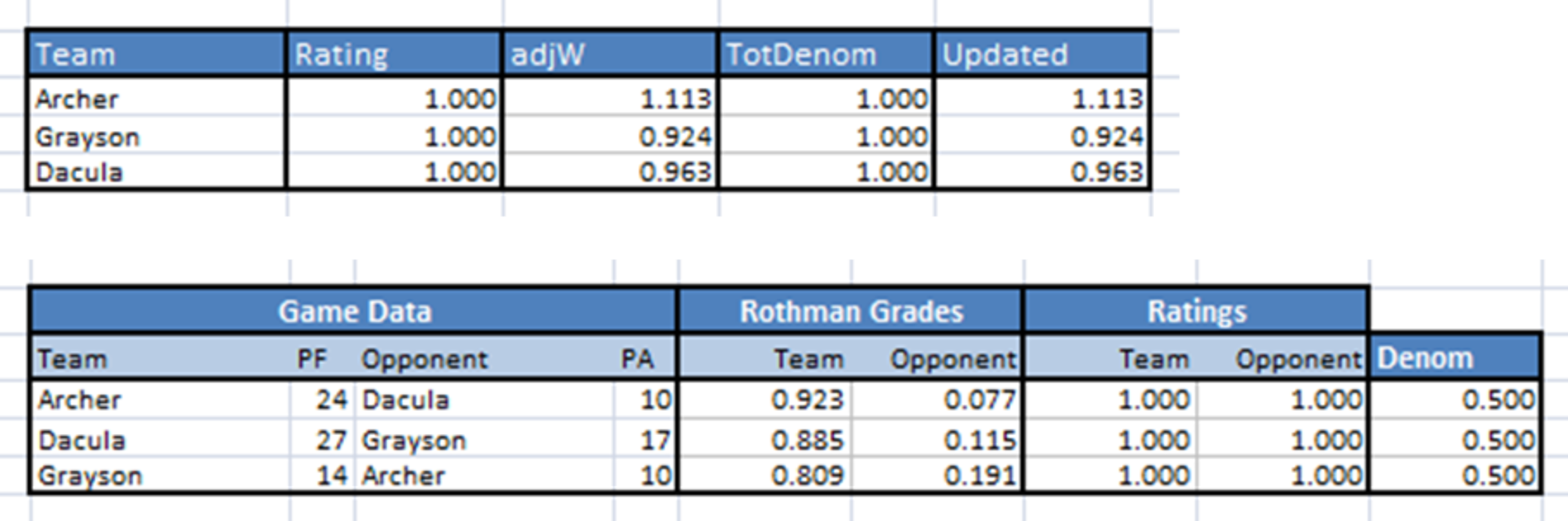
The next step is to update our Ratings by copying the Updated Rating to the Rating column in the teams table (I recommend using “Paste Values” if you’ve built this in Excel) and allow the effect of new rating to flow through the two tables:

Credit: Loren Maxwell

Credit: Loren Maxwell

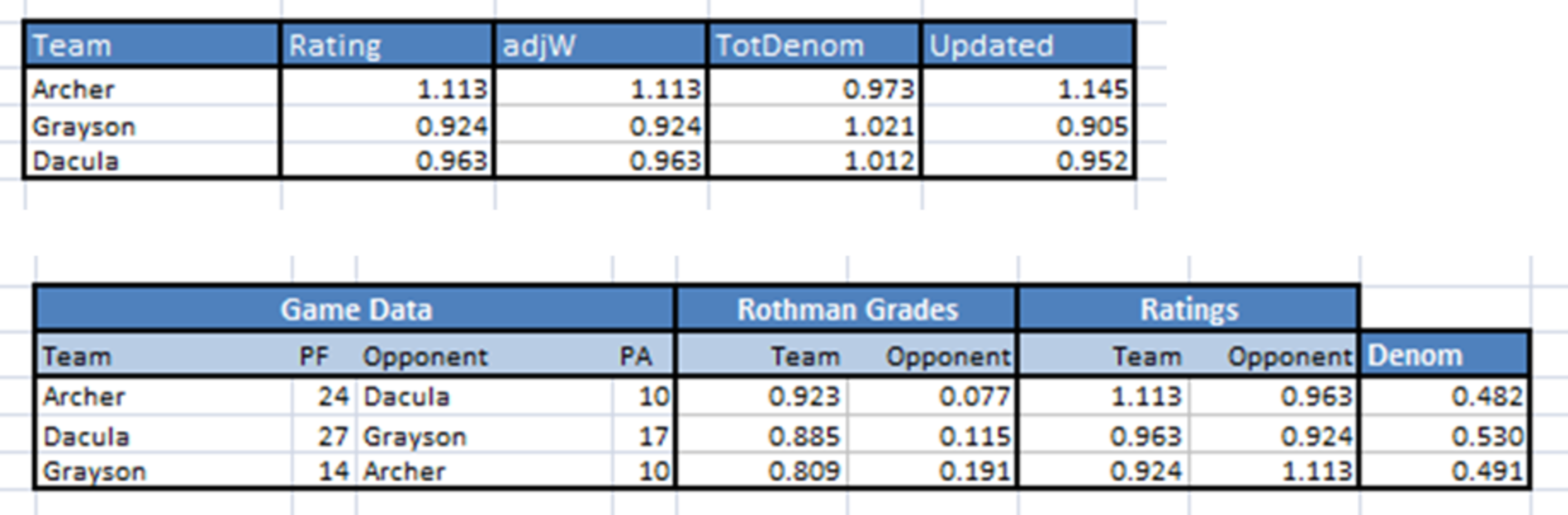
Let’s take a moment to follow the ripple effect of updating the ratings.

First, our new ratings are carried forward to the games table for each team and opponent.  For example, Archer's rating became 1.113 which is now reflected in their games against Grayson and Dacula.  This update causes the Denominator for each game to change. In turn, each of the teams now has a new Total Denominator in the teams table.  Finally, the Adjusted Wins, which remain constant, and the new Total Denominator are cranked through our B-T Update Function to generate a new Updated Rating.  In this case Archer's Updated Rating is 1.113 Adjusted Wins / 0.973 Total Denominator = 1.145.

This process constitutes a single iteration.

Let’s complete a total of ten iterations by repeatedly copying the Updated Rating to the Rating column and compare the changes in the team ratings through the iterations:

Credit: Loren Maxwell

Credit: Loren Maxwell

Note the changes in the ratings were larger at the beginning and got progressively smaller with each iteration. If we were just concerned with the first three decimal places of the ratings, then after the fifth iteration no further changes occur. In other words, the solution “converged” in five iterations.

Now, technically this is all that is required to run the complete B-T model – a method to assign a probability of preference between items (remember we used Rothman Grading) and then iterating the B-T Update Function until the solution converges.

However, by convention there are a couple of other simple steps performed to the ratings. Both steps are entirely cosmetic and only contribute to presentation of the ratings, not the mathematical rigor.

The first is a “normalizing” step, done by simply dividing each of the ratings by the lowest rating in the set. As mentioned above, by convention the lowest rating in the B-T model is 1, so this adjusts (or “normalizes”) the entire set of ratings so that the lowest rating returns to 1.

Using our example from above, Grayson’s rating is the lowest at 0.899, so dividing Archer’s rating by 0.899 normalizes it to 1.157 / 0.899 = 1.288 while Dacula's normalizes to 0.946 / 0.899 = 1.053.  Grayson's is simply 0.899 / 0.899 = 1.000.

This normalizing step can occur after the solution converges, such as in this simple example, or after each iteration.  Although here we'll do it after the solution converges, in practice I do it after every iteration in the Extended Standings.  Aside from the cosmetic benefit, it also avoids an extremely low rating from being rounded off to zero by the computer.

The second step is to present the rating as the natural logarithm of the actual rating. I realize mentioning logarithms can be intimidating, but here we simply use ln(rating) in Excel and we don't really need to understand or even use logarithms in the B-T model.

This is done because in large datasets the ratings for the top items can often be in the tens of thousands if not higher, so the natural logarithm of the actual rating makes the presentation cleaner.  For example, the natural logarithm of 100,000 is a much more manageable 11.513.

Since this number is not actually used in any way other than presentation, this step can be done after each iteration or when the solution converges.  In practice I simply have a column for it, so it automatically updates after each iteration.

Here’s our new team table with the “Normalized Rating” and “Presented Rating” columns included:

Credit: Loren Maxwell

Credit: Loren Maxwell

Finally, we can show the teams in terms of a complete round robin tournament againt every other team. Although in our simple example each team did in fact play all the others, for the most part this is not the case in football.

To calculate this number, we simply step through every team and calculate their “wins” and “losses” as compared to every other team using the B-T Probability Function from above. In the Extended Standings, I’ve termed these numbers as "xWins" and "xLosses".

So Archer’s xWins over Grayson would be:

A / (A + B) =

Rating of Archer / (Rating of Archer + Rating of Grayson) =

1.288 / (1.288 + 1.000) = 0.563

Using the same formula to compute Archer’s xWins over Dacula gives 0.550, so their total xWins would be 0.563 + 0.550 = 1.113.  Correspondingly Archer has 0.887 xLosses.

You might note that Archer’s xWins equals their Adjusted Wins, but this will only be the case where a round robin tournament has actually been played, such as in our three team example here.  In our Extended Standings this will give us the number of games each team would win if they were to play all 416 other teams in the GHSA.

So here is our final teams table, with an xWin% tacked on the end:

Credit: Loren Maxwell

Credit: Loren Maxwell

Now, I'm tempted to stop here for the day.  I've only introduced two simple formulas, the B-T Probability Function and the B-T Update Function, but they are sufficient to fully execute the B-T model on any set of data.

However, for readers looking for a little extra credit I'll quickly tie in Part V of the series by testing if the B-T Update Function actually produces the set of ratings that maximizes the likelihood of all the results. Zermelo, Bradley and Terry, and others have gone through the difficultly of developing the mathematical proofs for this, so here we won't be examining why the function works, only verifying it does.

Let’s add four columns to the games table.  The first two columns are straightforward, which is the B-T Probability for each team.  We can compute this using our B-T Probability Function from above, but observant readers might also note that since the Denominator is already 1 / (Team Rating + Opponent Rating) we could simply use Team Rating x Denominator and Opponent Rating x Denominator for these columns.

Here's our games table at the moment using the final ratings to calculate the B-T Probabilities:

Credit: Loren Maxwell

Credit: Loren Maxwell

Now let's add the last two columns, "Likelihood" and "Negative Log-Likelihood", and introduce another formula, our likelihood function:

(Team’s B-T Probability ^ Team’s Rothman Grade) x (Opponent’s B-T Probability ^ Opponent’s Rothman Grade)

For those interested, this is the binomial likelihood function with our Extended Standings terminology injected.

So, for Archer's game against Dacula, the likelihood would be:

(Archer's B-T Probability ^ Archer's Rothman Grade) x (Dacula’s B-T Probability) ^ (Dacula’s Rothman Grade) =

(0.550 ^ 0.923) x (0.450 ^ 0.077) = 0.542.

For reasons I'll explain in a moment, let's fill in the Negative Log Likelihood column with -ln(likelihood) for each game as well:

Credit: Loren Maxwell

Credit: Loren Maxwell

In theory, to measure how well the ratings fit all the data, we'd multiply all the likelihoods together to get the Product of Likelihood.  The goal under maximum likelihood is to find the set of ratings which results in the highest Product of Likelihood.

We're fine doing this for three games, but in reality this approach becomes impractical as the number of games increases.  To use the GHSA as an example, for 2,100 games this number will quickly approach so close to zero that the computer will simply round the result to zero.

So the standard approach is to instead use the negative log-likelihood.  Just as above, I won't get into logarithms here, but our goal under maximum likelihood becomes to find the set of ratings which results in the lowest negative log-likelihood.

Let's add two rows at the bottom of the games table showing both numbers:

Credit: Loren Maxwell

Credit: Loren Maxwell

Again, the Product of Likelihood is every Likelihood multiplied together, so in this case it would be 0.542 x 0.510 x 0.459 = 0.127, while the Sum of Negative Log-Likelihood is every Negative Log-Likelihood added together, 0.613 + 0.674 + 0.779 = 2.066.

Now, let's test the B-T Update Function by resetting all of our ratings to 1 again and look at the improvement in the Product of the Likelihood and the Sum of Negative Log-Likelihood at each iteration of updating the ratings:

Credit: Loren Maxwell

Credit: Loren Maxwell

Just as we had hoped, the Product of Likelihood gets larger with each iteration and correspondingly the Sum of Negative Log-Likelihood gets smaller.

In fact, we'll consider the solution to have converged once the change in the Sum of the Negative Log-likelihood is less than 0.00000001, so for this example we could consider the solution to have converged in the sixth iteration.

Now we can confidently say this set of ratings maximizes the likelihood of all the results.

So why is the ability to make this statement so important?

Because we're seeking to answer the question "Which teams are deserving of a playoff invitation?" and maximizing the likelihood demonstrates the B-T model possesses rigor, which translates into a sincere effort to find the answer through math.

WHEW!

Well . . . That's it for today.  If you're still reading then I appreciate you sticking with me through the full post and I encourage you to explore the B-T model more with different data sets and play around with what-if scenarios as you see fit.  In the end, it'd be great to have a knowledgeable base of individuals to check to ensure the Extended Standings meet our five characteristics as outlined in Part I.

Next time I'll cover the final component of the Extended Standings, which is showing how we can factor in a team's classification to offset the impact of relatively or completely isolated regions.  We'll also look at how the playoffs would have been seeded if the Extended Standings had been used over the last few years.

Thanks again for reading and I look forward to hearing your thoughts!